Student Lead: Simon Olofsson
Summary
This project looks at optimising a combination of conflicting black-box and analytical objective functions. Two existing Bayesian methods are adapted and compared to each other and to competing multi-objective optimisation methods.
What is the challenge?
With multiple conflicting objective functions, it becomes difficult to define what constitutes an optimal solution. The goal is to find a good trade-off between the objectives. There are two distinctly different methods to do this: (i) scalarisation, where the trade-off is made a priori (beforehand) by choosing an aggregated, scalarised function, e.g. a weighted sum, which is then optimised, and (ii) the Pareto method, where optimisation is used to find the best approximation of the optimality curve (Pareto frontier) in objective space, and the trade-off is made a posteriori (afterwards) by selecting the most satisfying point on this curve.
Scalarisation is easy to employ, but introduces a new problem in the choice of aggregated function and weights, which have to be chosen a priori, often with incomplete understanding of how the system performs. Additionally, not all solutions can be found using scalarisation – e.g. a weighted sum aggregated function can only find solutions lying on convex sections of the Pareto frontier. The Pareto method, on the other hand, suffers from the limitation that it becomes difficult to choose an optimal solution a posteriori when the objective space is high-dimensional and hard to visualise.
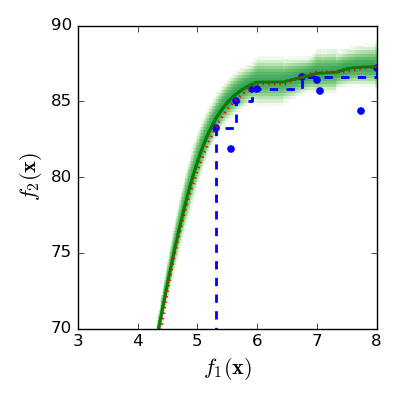 What contributions have we made?
What contributions have we made?
We look at an application with one black-box objective function of neotissue growth in a bioreactor, and one analytical objective function of the cost of growing the tissue. We adapt two existing acquisition functions (expected hyper-volume improvement, and expected maximin improvement) for Bayesian multi-objective optimisation to the scenario of combined black-box and analytical objective functions.
We show that the two Bayesian acquisition functions perform equally well, and that they out-perform the NSGA-III evolutionary algorithm in five test problems as well for the tissue engineering application. Furthermore, we show that sampling from the posterior to compute a probabilistic Pareto frontier can give valuable information about unexplored optimal solutions even after the optimisation algorithm finishes.
Collaborators
- Dr Liesbet Geris & Mohammad Mehrian (Tissue engineering)
- Dr Roberto Calandra (Bayesian optimisation)
- Dr Marc Peter Deisenroth (Bayesian optimisation)


