Student Lead: Radu Baltean-Lugojan
Summary
This project investigates using problem structure for finding globally optimal solutions in non-convex optimisation. We analyse specific problem structure in volatility modelling (finance) and in pooling networks (oil & gas).
Background & Challenges
A wide range of theoretical and industrial applications of optimisation go beyond linear or convex problems and fall in the category of non-convex optimisation. Solving such problems implies multiple local optimal solutions, rendering gradient-based search unable to deterministically find the global optimal solution. Multiple frameworks for deterministic global optimisation have been proposed and implemented in academic and commercial solvers, most notably branch-and-bound or branch-and-cut.
However, existing approaches do not scale well to relevant large-scale problems which are often NP-Hard. In general, the more problem structure an optimisation solver is able to incorporate the more computationally efficient it becomes. Finally, there is a trade-off between using very specific problem structure (in analytical, topological or polyhedral form) and maintaining generality.
Our Contributions
Piecewise Parametric Structure in the Pooling Problem (topological and analytical piecewise structure)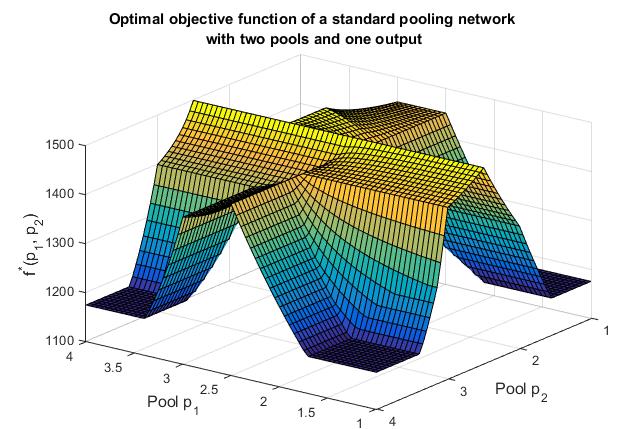
The standard pooling problem is a NP-hard sub-class of non-convex quadratically-constrained optimization problems that commonly arises in process systems engineering applications. We take a parametric approach to uncovering topological structure and sparsity of the standard pooling problem in its p-formulation. The structure uncovered in this approach validates Professor Christodoulos A. Floudas’ intuition that pooling problems are rooted in piecewise-defined functions. We introduce dominant active topologies to explicitly identify pooling problem sparsity and show that the sparse patterns of active topological structure are associated with a piecewise objective function. Finally, the paper explains the conditions under which sparsity vanishes and where the combinatorial complexity emerges to cross over the P/NP boundary. We formally present the results obtained and their derivations for various specialized pooling problem instances.
Non-linear calibration of implied volatility expansion models (algebraic structure approximation)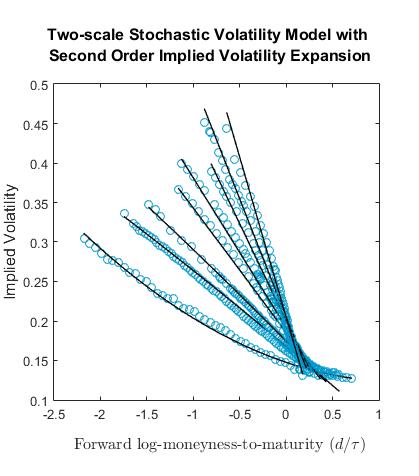
Implied volatility expansions allow calibration of sophisticated volatility models. They provide an accurate fit and parametrization of implied volatility surfaces that is consistent with empirical observations. Fine-grained higher order expansions offer a better fit but pose the challenge of finding a robust, stable, and computationally tractable calibration procedure due to a large number of market parameters and nonlinearities. We propose calibration schemes for second order expansions that take advantage of the model’s structure via exact parameter reductions and recoveries, reuse and scaling between expansion orders where permitted by the model asymptotic regime, and numerical iteration over bounded significant parameters. We perform a numerical analysis over 12 years of real S&P 500 index options data for both multiscale stochastic and general local-stochastic volatility models. Our methods are validated empirically by obtaining stable market parameters that meet the qualitative and numerical constraints imposed by their functional forms and model asymptotic assumptions.
Publications
- R. Baltean-Lugojan, R. Misener, Piecewise Parametric Structure in the Pooling Problem – from Sparse Strongly-Polynomial Solutions to NP-Hardness, submitted to journal, 2017.
- R. Baltean-Lugojan, P. Parpas, Robust numerical calibration for implied volatility expansion models, SIAM Journal on Financial Mathematics, volume 7, issue 1, pp.917–946, 2016.


