Summary
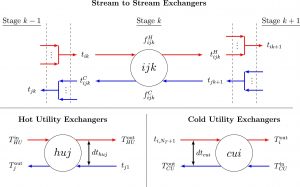
Many industrial processes involve heating and cooling liquids: a quarter of EU energy consumption comes from industry and industry uses 73% of its energy on heating and cooling (European Commission, 2016). With the present focus on reducing CO2 emissions, e.g. the UK Climate Change Act 2008, reusing excess process heat becomes ever more important. Heat exchanger networks reuse excess heat onsite and thereby minimise cost and improve energy recovery in chemical processes. The heat exchanger network synthesis problem optimises the superstructure, e.g. decides which hot streams i to match with cold streams j.
What is the challenge?
Heat exchanger network synthesis is a mixed-integer nonlinear optimisation problem. The discrete aspect comes from deciding whether a heat exchanger exists or not. The nonlinearities arise from:
- Stream mixing When process streams of the same phase but different temperatures mix, the result is a set of non-convex bilinear terms equivalent to those in the pooling problem.
- Nonlinear nature of heat exchange The logarithmic mean temperature difference function LMTD(x, y) = (x – y)/ln(x/y), which characterises heat transfer, is undefined when x = y.
- Heat exchanger area calculation The size of a heat exchanger scales (i) proportionally with the heat load exchanged between two streams and (ii) inversely with LMTD.
- Concave cost function The cost of a heat exchanger scales as the area raised to a power β, typically β = 0.6 or 0.7.
It is already known that a linear version of heat exchanger network synthesis, i.e. one including the discrete aspect but neglecting the nonlinearities, is NP-hard. The nonlinear version of this problem incorporates the pooling problem, which is also known to be NP-hard.
What contributions have we made?
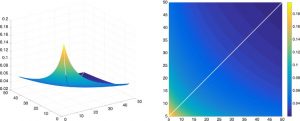
Convexity properties of the logarithmic mean temperature difference function
Mistry & Misener, Computers & Chemical Engineering, 2016
The logarithmic mean temperature difference (LMTD) function was previously associated with numerical difficulties. But after adding the limits, we prove the strict convexity of LMTD^β, β < 0, and also characterise the shape of the function for all β ≤ 1. These proofs motivate why previous, heuristic-based approaches work best when the problem is reformulated to move the LMTD terms into the objective. Here is the LMTD function for β = -1:
Heuristics with performance guarantees for the minimum number of matches
Letsios, Kouyialis & Misener, Computers & Chemical Engineering, 2018
Heat recovery network synthesis remains a difficult optimisation problem with many nonconvex nonlinearities. The sequential method generates good solutions by decomposing the original mixed-integer nonlinear optimisation problem into: (i) minimising utility cost, (ii) minimising the number of matches, and (iii) minimising the investment cost. The sequential method may not return the global solution of the original problem, but solutions generated with the sequential method are practically useful (Floudas et al., AIChE J, 1986).
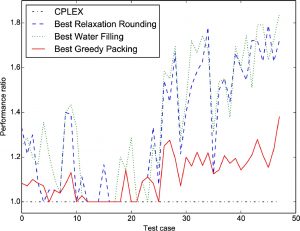
Minimising the number of matches, i.e. minimising the number of required heat exchangers, is a sequential method bottleneck, so we consider three classes of heuristics:
- Relaxation rounding heuristics consider an efficiently-solvable relaxation of the original mixed-integer optimisation problem that allows violation of certain constraints. The resulting solutions are rounded to feasible solutions for the original problem.
- Water filling heuristics iteratively produce a solution by exchanging the heat in a series of smaller problems.
- Greedy packing heuristics start from an infeasible solution with zero heat transferred between the streams and iterate towards feasibility by greedily selecting matches.
We explore these three classes of heuristics theoretically and computationally. For 48 literature test cases with 43 streams or fewer, this line chart compares the performance ratio, i.e. computed solution / best known solution for the relaxation rounding, water filling, and greedy packing methods. For larger problems, our methods continue to efficiently produce good solutions whereas exact methods become weak.
Beyond approximation algorithms, our work has interesting implications for solving the minimum number of matches problem exactly, e.g. the analysis into reducing big-M parameters or the possibility of quickly generating good primal feasible solutions.


