Student Lead: Francesco Ceccon
This project is open source. Please find the GitHub repository here.
Summary
This project detects pooling problem structures within nonconvex mixed-integer nonlinear optimisation problems. Finding named structures allows us to apply cutting planes or primal heuristics specifically designed for pooling problems.
Background & Challenges
The pooling problem is an industrially-relevant nonconvex nonlinear optimisation problem minimising cost on a feed-forward network of input nodes, intermediate storage or pool nodes, and output nodes. Variants of the pooling problem have applications such as crude oil scheduling. The difficulty of the pooling problem arises from the nonconvex bilinear terms representing linear blending in the pools. These bilinear terms, which are necessary for tracking quality across the network, typically multiply flow rates and concentrations or flow fractions.
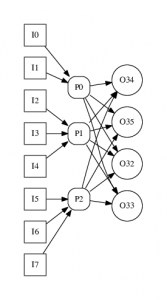
Previous work on mixed-integer optimisation has found that using network structure can significantly help generate strong cutting planes. Automatically identifying these embedded networks in large-scale optimisation models is NP-hard, but there exist several polynomial time approximation algorithms to find good networks. State-of-the-art MIP solver software, including MINTO and CPLEX use preprocessing heuristics to automatically find these network patterns. More recent work has considered detecting more complex structures such as multi-commodity flow and recovering variable meaning from flat MIP structures.
Due to nonlinearities, deterministic global optimisation solvers do not
currently infer pooling network structure and therefore will solve the pooling problem and its variants via branch-and-cut on the McCormick bilinear convex hull.
Contributions
This project proposes a method to automatically recognize pooling structure within a mixed-integer nonlinear optimisation problem. This can be seen as a three step process: first we convert the problem from one of the existing formulations (P, Q, and PQ formulations) to a canonical PQ-formulation, then we recognize the named structure in the flat mixed-integer nonlinear problem, and finally we reconstruct the pooling problem network.
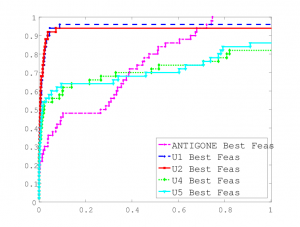
We tested the proposed method on three datasets: 70 large scale standard
pooling problems by Dey and Gupte, 16 standard and extended pooling by Misener et al., and the 1342 MINLPLib2 test cases. We can detect all standard and extended pooling problems in the first two datasets, and find pooling networks in 6% of MINLPLib2. After detecting the pooling problem in the MINLP, we can apply an heuristic approach to get a good approximation solution.


