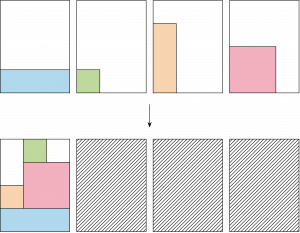Summary
The project investigates how to use satisfiability modulo theories, an approach commonly used in software verification contexts, to accelerate mixed-integer programming solution methods.
Background and Challenges
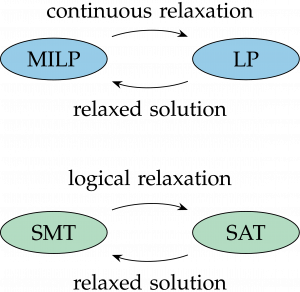
Optimisation problems often involve logical/discrete decisions, e.g. assignment or existence, as well as mathematical constraints. A mixed-integer approach relaxes these discrete decisions to a continuous representation which can cause a partial loss of logical structure but leverages powerful (non)linear programming solvers. A satisfiability modulo theories (SMT) approach instead relaxes the mathematical theory to a Boolean representation which causes a loss of mathematical structure but leverages powerful Boolean satisfiability solvers.
SMT methods support incremental solving and logical reasoning of infeasible solutions by learning conflict constraints that aid searching. Integrating these methods into mixed-integer solving comes with the challenge of (i) modelling so that we may easily detect and leverage logical structures that are present, (ii) tracking the logical implications of search decisions, and (iii) converting SMT-like conflict clauses into mathematical inequalities without excessive increase in the mixed-integer model.
Contributions
We developed an SMT based branch-and-bound algorithm for the two-dimensional bin packing problem which, given identical bins, finds the minimum number of bins needed to pack a set of rectangles without rotation or overlaps.
Our method uses an SMT solver throughout the algorithm. Iterations of the algorithm reduce the number of available bins to leverage SMT unsatisfiable cores which, in this context, correspond to subsets of rectangles that cannot be packed in the reduced number of bins. These unsatisfiable cores derive branching choices and symmetry breaking clauses. We eliminate further symmetries that arise as a result of the algorithm’s wide branching strategy with additional clauses. We compare our approach to state-of-the-art MINLP solvers on the Berkey and Wang (1987), and Martello and Vigo (1998) test library.