Summary
In many engineering applications, accurate mathematical modelling requires discrete decisions and non-linear relationships. Optimising these models is most flexibly done using mixed-integer nonlinear programming (MINLP). Deterministic global optimisation of MINLP is valuable for a range of industrial applications including and energy systems and biological and biomedical systems.
But there is an enormous gap between what should be computationally tractable and what MINLP computational tools are currently capable of addressing. Our work synthesises general mathematical advances and individualistic problem-specific knowledge into effective algorithmic protocols and computational tools for solving MINLP. Beyond creating tools, we introduce and develop innovative applications opening new domains for computational optimisation.
What is the challenge?
Consider a toy MINLP with one continuous variable (x1 ∈ [0, 1]), one discrete variable (x2 ∈ {0, 1, 2, 3, 4}), a linear objective function (x1 + x2), and two nonlinear constraints:

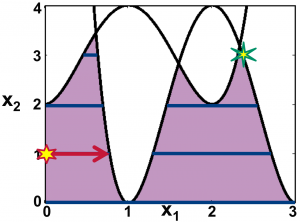
The solution point is the green star in the upper right-hand corner; this is the point within the feasible space (denoted by dark blue lines) with the greatest value of x1 + x2. But it is possible that a local solution method may initialise at a point such as the red star in the lower left of the figure; a local search staying within the feasible space would not reach the global solution.
This is a toy problem; research has pushed the state-of-the-art to the point where ANTIGONE (Misener and Floudas, 2014) can address several bench-marks up to O(10^4) variables and equations. In practice, solving MINLP is tractable via heterogeneous algorithms pieced together into a framework; we develop and integrate complementary algorithmic components.
What contributions have we made?
Given user-defined MINLP, the ANTIGONE framework we developed reformulates the model, detects special mathematical structure, solves the optimization problem, and returns the model with respect to the original variables (Misener and Floudas, 2014).
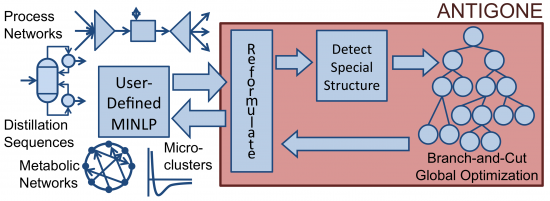
Following are some of the other items we have previously investigated; see our publications for more!
- Proposed automatic preprocessing reformulations including disaggregating bilinear terms and flattening the directed acyclic graph of nonlinear functions;
- Explored facet properties of low-dimensional (n ≤ 3) edge-concave aggregations admitting a vertex polyhedral convex hull and extended this analysis to higher dimensions;
- Developed a corollary to Crama’s [Math Program, 61:53–60, 1993] necessary and sufficient condition for the existence of a cut dominating the termwise relaxation of a bilinear expression; the corollary screens whether the minimum necessary difference is zero or not;
- Designed a framework for practically introducing four classes of cuts including: (1) RLT equations; (2) supporting hyperplanes for convex univariate quadratics and convex multivariable terms; (3) aBB cuts; (4) high-dimension edge-concave facets. We try to generate the computationally inexpensive cuts first;
- Released our advances as publicly available solver software (ANTIGONE and GloMIQO).
Where do we go from here?
We have lots of challenging applications which push the limits of available solution strategies; consider working with us! We continue our drive towards developing innovative algorithms and numerical techniques for MINLP.
Collaborators
- Prof Christodoulos A Floudas (PhD advisor)
- Dr Michael Bussieck, Dr Stefan Vigerske (software development mentors)
- Dr Anders Skjäl, Prof Tapio Westerlund (αBB Underestimators)
- Prof Chrysanthos Gounaris (piecewise linear underestimators)
Software
- ANTIGONE (Solves Mixed-Integer Nonlinear Optimisation Problems)
- GloMIQO (Solves Mixed-Integer Quadratically-Constrained Quadratic Optimisation Problems)


